Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.
Falar sobre a teoria dos grafos aqui no blog é falar sobre um tema que já estudamos várias vezes. Então por abordar novamente? Acho que uma postagem dedicada é válida, pois até o momento só olhamos os grafos por uma determinada ótica, da forma computacional, mas existem várias outras que ainda não exploramos. Logo, minha expectativa é que aqui possa ser um ponto de partida para vários outros assuntos.
Um dos pontos que ainda não foi explorado é a aplicação real da teoria dos grafos na nossa realidade, ou seja, no nosso dia a dia. Se você se vê obrigado a ter de estudar este assunto por causa de obrigações acadêmicas, pode acabar se perguntando: para que serve isso ? onde é usado ?
A resposta pode parecer assustadora, mas você usa a teoria dos grafos frequentemente e não se dá conta disso. Diversas são as aplicações para este ramo da matemática:
- Geolocalização: GoogleMaps e Waze
- Compactação de arquivos
- Estruturas de dados
- Ponte área entre cidades
- Planejamento de uma viagem em família
- Grade das suas matérias na faculdade
Quando você está no aeroporto e olha a escala de vôos pode acabar se perguntando: como é possível determinar se um avião que sai de São Paulo pode ou não passar por Fortaleza ? Mais uma vez, a teoria dos grafos está aí. Baseado nesta mesma idéia, o GoogleMaps e Waze funcionam da mesma forma. Como é possível determinar um trajeto de um ponto a outro em um mapa, e ainda respeitando ou não o sentido de ruas ? O sistema operacional que você usa utiliza árvores B para organizar/trazer grandes blocos de informações em disco, como ele faz isso ? Acredito que nesta altura a resposta para todas essas perguntas já esteja clara.
Embora essa teoria parece ser algo dos últimos 40 ou 50 anos, na verdade ela é bem mais antiga que isso. Sua origem data do ano de 1736, onde o grande físico e matemático Leonhard Euler resolveu o problema das Sete Pontes de Königsberg com a construção de um grafo, o qual mostrava que o boato popular de percorrer todas as pontes passando uma única vez era impossível, pois a disposição existentes dos elementos não possibilitava tal (NETTO, PAULO OSWALDO). No problema estudado, os pontos correspondiam a margens do rio, e as arestas, as pontes.
Este grafo deu origem a esse novo campo da matemática e se tornou o primeiro grafo desenhado conhecido.
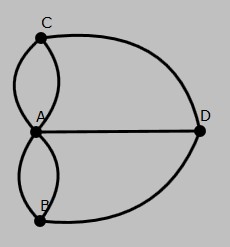 |
| Figura 1 - O grafo-solução do problema das Sete Pontes de Königsberg |
-----------------------------------------------------------------------------------------------------------------------
Nota: Você sabia que a palavra Königsberg vem da língua germânica e significa "montanha do rei" ?
-----------------------------------------------------------------------------------------------------------------------
Tá, tudo bem mas o que é um grafo ?! 😕
Matematicamente um grafo é um conjunto. Essa representação gráfica usada com bolinhas e linhas, conhecidas respectivamente como nós ou vértices e arestas, é para facilitar a visão sobre um problema. Então, é possível concluir que um grafo é um conjunto de vértices e arestas. Aplicando este conceito no grafo mostrado na Figura 1, teríamos:
Onde G é o grafo e, V e A são conjuntos. V é o conjunto de vértices do grafo. Entenda um vértice como um ponto de interseção entre arestas. Logo paga G temos:
O conjunto de arestas, representado por A, é composto de:
Note que as arestas são formadas pelos vértices que a compõem, logo AB significa que existe uma aresta que sai do vértice A e vai para o vértice B. Mas nada impede que você nomeie cada uma e tenha no final algo assim:
O grafo mostrado na Figura 1 é bem básico, e como dito anteriormente, essa postagem será o ponto de partida para vários outros conceitos que ainda estão por vir, como: buscas, matrizes, atribuição de direções ou pesos para as arestas, árvores, árvores geradoras, etc. Todas esses novos conceitos serão abordados em postagens futuras.
Note que esta postagem não segue o padrão de postagens do blog. Não introduzimos nenhum algoritmo ou código-fonte. Optei por esse modelo para que o assunto pudesse ser apresentado de uma forma leve ao leitor.
Terminamos !!! 😆👍
Até a próxima ! 😘
Leia nossa próxima postagem: Matrizes de adjacência e grafos
Referências
NETTO, PAULO OSWALDO; Teoria e Modelos de Grafos; 1979

Nenhum comentário:
Postar um comentário