Preciso estudar sempre: O código de Huffman

Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.

Você já parou para pensar como os programas de compressão de dados, como WinZip, WinRar, GZIP, entre outros conseguem diminuir o tamanho de um arquivo ? Como será possível diminuir um arquivo de 1Gb para 600 Mb sem perder a informação contida ali ?

Em 1952, David A. Huffman criou o código de Huffman [1] com o intuito de construir um código binário de redundância mínima mais eficiente do que de seu professor, Roberto M. Fano [2]. Através de sua criação se tornou possível a realização de compressões utilizando combinações mínimas de códigos binários não redundantes, ou seja, que não se repetem.

Figura 1 - David Albert Huffman

Mas porque comprimir dados é algo tão importante ?

Pense na seguinte situação: você tem que enviar alguns dados via internet, mas sua conexão é instável, cai toda hora e você não pode enviar pacotes muito grandes, pois podem haver problemas de falta de informação. Então, o que você faz ? Não envia os dados ? Neste tipo de situação a compressão de dados pode ser uma bela mão na roda.

Para que possamos realizar a compressão dos dados utilizando o código de Huffman, devemos primeiro montar uma tabela com duas colunas. A primeira coluna contém os caracteres usados no texto enviado, e a segunda os códigos binários que representam cada caractere. Contudo, você lembra no início do post que eu citei que o código de Huffman é redundância mínima ? Essa redução de redundância significa que cada caractere se transforma em um código binário único.

Para fins de exemplo em todo o post utilizaremos o seguinte texto como exemplo:

"o rato roeu a roupa do rei de roma"

Para cada caractere utilizado um código binário único é associado a ele, ou seja, a letra "o" poderia ser 00, o "b" 10, ou o "a" 11. Porém, é importante ressaltar que nenhum código pode conter outro, por exemplo: se a letra "b" é 10, a letra "r" não pode ser 1000, pois se fosse haveria um problema grande no momento de descompressão. O que seria "r" e o que seria "b" ? Nenhum código pode ser unicamente 0 ou 1 também, pois isso eliminaria toda a gama de combinações binárias possíveis que começam com estes dois números.

Mas uma pergunta permanece: onde está a compressão nisso tudo ? Em modelos como ASCII ou o Unicode, todos os caracteres mapeados por tais possuem, respectivamente, 1 e 2 bytes. Então o nosso texto codificado em um desses modelos seria uma sequência de 0 e 1.

1 byte = 8 bits

2 bytes = 16 bits

A resposta se tornou clara. Se no melhor dos cenários, o modelo ASCII, mapeia cada caractere como 8 bits e conseguimos diminuir essa quantidade para 2 bits, está aí a compressão.

A tabela citada no parágrafo acima é o resultado final do algoritmo do código de Huffman, ela acaba atuando como uma cifra, pois através da mesma é possível comprimir e descomprimir qualquer caractere do texto enviado. Então, tais tarefas que pareciam ser extremamente complicadas acabam se tornando algo simples pois, somente precisamos ler cada caractere e achar seu correspondente binário para comprimir, e para o processo reverso, analisar cada binário e ver sua correspondência em caractere.

Mas como construir a tabela ? A resposta reside em uma árvore binária completa, onde nas folhas ficam os caracteres do nosso texto. Se você nunca leu nada sobre árvores binárias, clique aqui ou dê uma olhada na postagem feita aqui no blog sobre árvores binárias. O link estará no fim desse post.

Para montar a árvore é necessário analisar o texto a ser processado. Note que algumas letras se repetem como o "o", "i", "e", "b", entre outras. O primeiro passo que devemos tomar é montar uma relação de todas as letras usadas, onde cada uma deve vir acompanhada com a quantidade de vezes que se repete. A Tabela 1 mostra a relação montada para o texto de exemplo.

Tabela 1 - Mapa de caracteres com suas quantidades

Note que a relação está ordenada de forma ascendente pela quantidade de cada letra e isso é importante porque como veremos adiante está ordem é determinante para a execução do algoritmo. É de alta importância ressaltar que o caractere whitespace também é contabilizado na nossa análise, pois quando o texto for descomprimido queremos que o texto de saída seja igual ao de entrada. Com a relação pronta podemos montar a árvore binária, seguindo os passos abaixo.

Passo 1: Utilizando a Tabela 1, transforme todas as letras e suas respectivas quantidades em raízes de árvores binárias. Por uma questão de simplicidade de representação iremos utilizar essa bolinhas para representar os nós da árvore e o número abaixo de cada uma é a quantidade de repetição de cada letra.

Figura 2 - Passo 1 da construção da árvore binária de Huffman

Passo 2: Pegue os dois primeiros nós, e transforme eles em filhos de um novo nó, onde a quantidade de repetição desse novo nó é a soma das quantidades de seus filhos. Como este novo pai não possui caractere, seu conteúdo será em branco. Lembre-se de como as árvores binárias funcionam, menores à esquerda e maiores à direita.

Figura 3 - Passo 2 da construção da árvore binária de Huffman

Passo 3: Reordene os nós pela quantidade de repetição de forma ascendente.

Figura 4 - Passo 3 da construção da árvore binária de Huffman

Passo 4 até 10: Repita os passos 2 e 3 até que sobre somente um único nó.

Figura 5 - Passo 4 da construção da árvore binária de Huffman

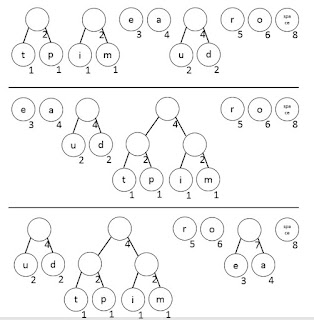Figura 6 - Passo 5 da construção da árvore binária de Huffman

Figura 7 - Passo 6 da construção da árvore binária de Huffman

Figura 8 - Passo 7 da construção da árvore binária de Huffman

Figura 9 - Passo 8 da construção da árvore binária de Huffman

Figura 10 - Passo 9 da construção da árvore binária de Huffman

Figura 11 - Passo 10 da construção da árvore binária de Huffman

Não há muito o que explicar aqui, pois as imagens já fazem esse trabalho. Note que o processo de criação da árvore de Huffman é algo bem simples e como resultado todos os caracteres acabam virando nós folha. Lembre-se deste fato, pois ele será de extrema importância na montagem da implementação em Java do nosso algoritmo.

Visto que já abordamos o processo de criação da árvore, podemos começar a abordar o processo de criação da sequência binária. É bem simples de fato. Para cada caminho à esquerda tomado é acumulado 0 ao resultado final, e para cada caminho à direita é acumulado 1. Então, utilizando a Figura 11 podemos concluir que o caractere 'e' é igual à 000, o 'a' 001, o 'p' 10101 e assim segue até o último. Faça o teste, gere todos os códigos de todos os caracteres e conclua que o que foi dito no início do post é de fato verdade. Nenhum código consegue ser contido em outro, por isso é importante que os caracteres sejam as folhas desta árvore.

Como já disse em outras postagens, utilizo Java para a implementação do que estou abordando por uma questão de afinidade, mas nada impede que você recrie a mesma situação na linguagem de sua preferência. Vamos analisar o código parte por parte.

A classe HuffmanNode dispensa comentários complexos. Ela é uma simples classe com alguns atributos e getters e setters. Dentre estes atributos os que merecem mais atenção são: isLeaf e frequency. O primeiro representa um booleano que determina se um nó é folha ou não, criado para tornar a leitura do código melhor. O segundo é a frequência de repetição já citada anteriormente. Os demais atributos são os que tornam a classe um nó de uma árvore binária, ou seja, uma referência para um possível filho à esquerda ou à direita e um valor inteiro para o conteúdo.

Note que eu disse "valor inteiro" e não "caractere". Porque isto acontece se nossa árvore contém letras nas extremidades ? Em Java, e acredito também que em outras linguagens, é possível transformar valores inteiros em caracteres e vice-versa. Isto se dá pelo fato de todo caractere ser internamente um número na tabela ASCII ou no modelo Unicode. Deixarei na seção Outros links o link para a tabela ASCII, onde é possível ver todos os códigos numéricos de todos os caracteres. Faça o teste em casa. 😀

Preferi utilizar esta abordagem por uma questão de conforto, pelo fato de que é difícil identificar onde está o nó space, e também é uma forma de "marcar" os nós sem conteúdo. Veremos este ponto adiante.

Abaixo, a classe que representa a árvore.

Se concentre nos seguintes tópicos listados abaixo:

O atributo root - Representa a raiz da nossa árvore. É através dela que começamos qualquer busca. É a única referência existente a um nó.
Método getCharFrequency - Monta a relação de caracteres e suas respectivas quantidades de repetição, assim como a Tabela 1 também mostra. Esta relação serve de entrada para a montagem da árvore.
Método createBinaryMap - Monta uma relação de caracteres e suas respectivas sequências binárias, onde as sequências somente serão alimentadas após o processamento da árvore. Esta relação é o resultado do processamento feito pela árvore.
Método initializeTree - Cria a lista de raízes.
Método createTree - Executa todo o procedimento explicado pelas Figuras 2 até 11. Seu parâmetro de entrada é a lista gerada pelo método initializeTree.
Método crypt(String nonCryptedText) - Representa a interface pública para a compressão de dados. Sua responsabilidade é receber um texto não comprimido, realizar a compressão e retornar sua versão compactada.
Método crypt(HuffmanNode root, String currentBinary, Map binaryMap) - Versão sobrecarrega do método crypt. Realiza a busca recursiva na árvore, começando da raiz e indo até as folhas. Os três parâmetros são necessários, pois como é baseado em recursividade, o parâmetro root é atualizado constantemente, a atual sequência binária também é atualizada de acordo com o caminho tomado, e o mapa é utilizado para armazenar a sequência a partir do momento que uma folha é atingida. Note que este método não procura somente um único caractere, e sim todos. A árvore é vasculhada completamente.
Método decrypt - Sua responsabilidade é receber um texto comprimido e retornar sua versão descompactada. Tal é realizado utilizando a tabela resultado montada no processo de compressão.

Como utilizar ?

Note que a utilização é bem simples. Caso você queira comparar resultados de tamanho de arquivo antes e depois da compactação, siga as seguintes instruções:

Visite o site http://br.lipsum.com/
Gere um texto com 1000 palavras
Guarde esse texto um novo arquivo txt
Gere o código binário a partir do texto através de algum conversor online. Guarde o resultado em um novo arquivo txt
Inicie o programa de compactação passando como entrada o texto gerado
Aguarde pelo resultado, copie o código binário compactado gerado e cole em um novo arquivo txt
Analise o tamanho dos dois arquivos, a versão binária não compactada e a compactada, e veja a diferença de tamanho entre eles. Caso você fique com dúvidas sobre a integridade do conteúdo compactado, realize a descompressão e compare os resultados. O texto descompactado deve ser igual ao gerado pelo site da etapa 1.

Seguindo estas instruções, obtive o resultado mostrado pela Figura 12.