Inserindo as coisas certas nos lugares certos - O algoritmo Insertion Sort

Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.

Este é mais um post da série de algoritmos de ordenação que já vínhamos estudando aqui no blog. Diferentemente do último post (você pode dar uma olhada clicando no link abaixo), este algoritmo é mais fácil pois não envolve recursão mas, é um pouco mais complicado que seus primos Bubble Sort e Selection Sort (falaremos dele futuramente).

Dividindo e conquistando - O algoritmo Merge Sort

Mas qual é a idéia central sobre esse algoritmo ? Sob quais circunstâncias ele funciona ? Perguntas como essas e outras devem estar passando na sua cabeça agora visto que, esse algoritmo não é muito conhecido por aí.

Imagine a seguinte situação: você está jogando uma inofensiva partida de sueca com seus amigos, o baralho foi cortado e as cartas foram dadas. Você pegou sua mão e isso é o que veio.

Figura 1 - Sua mão de cartas

Sua reação:

Figura 2 - Sua reação

Não queria te falar mas você vai tomar uma surra.

É possível notar que algumas dessas cartas já vierem ordenadas. Isso foi feito propositalmente. Veremos adiante que esse algoritmo tem uma melhor performance se executado em conjuntos previamente ordenados. Você pode estar pensando que isso é óbvio visto que, se parte do conjunto já está em ordem, você já fez parte do trabalho para o algoritmo. Errado. Se você conhece o algoritmo Bubble Sort, sabe que ele não considera conjuntos pré-ordenados.

Caso não conheça ou queira relembrar, dê aquela clicada aqui.

O algoritmo Insertion Sort executa em tempo O(N²) mas é cerca de duas vezes mais rápida que o Bubble Sort e um pouco mais rápido que o algoritmo Selection Sort. Sua idéia central é que um marcador seja posto em um elemento onde, todos os elementos à esquerda do marcado estejam ordenados e todos à direita estejam desordenados. No nosso exemplo, o elemento marcado é o cinco de espadas e, é possível notar que ele atende aos pré-requisitos.

Pergunta: é viável aplicar o algoritmo Insertion Sort em um conjunto de dados completamente desordenado ?
Resposta: Sim, é. Com o conjunto nesse estado, o elemento marcado será o primeiro visto que, a esquerda dele não existem elementos e à direita dele, todos estão desordenados.

A partir do momento que elegemos a carta marcada, precisamos executar os seguintes passos:

1. Retirá-la do conjunto.
2. Achar qual é seu lugar no sub-conjunto ordenado.
3. Deslocar algumas cartas para a direita para que possamos reposicioná-la.
4. Mover marcador 1 passo para a direita.

Senão entendeu, acompanhe o passo-a-passo.

Figura 2 - Passo-a-passo do algoritmo

A próxima carta, nove de espadas, já está na ordem então o algoritmo pula está carta e marca a próxima. Este processo é repetido até todo o conjunto estar ordenado.

1:  private void sort(int[] values){  
2:       int i,j;  
3:    
4:       for (i=1; i<values.length; i++) {  
5:            int temp = values[i];  
6:            j = i;  
7:            while(j>0 && values[j-1] >= temp){  
8:                 values[j] = values[j-1];  
9:                 --j;  
10:            }                 
11:            values[j] = temp;  
12:       }  
13:  }  

A implementação acima representa o algoritmo. O primeiro laço começa com o contador em 1 porque, como já havíamos discutido, o marcador deve estar no primeiro elemento desordenado à direita do sub-conjunto ordenado, ou seja, o segundo elemento do conjunto. O primeiro elemento pode estar até desordenado analisando o todo, mas nessa etapa o sub-conjunto de elementos ordenados só tem um elemento. Logo, ele está ordenado.

O elemento marcado é copiado para uma variável temporária e é verificado se o elemento anterior à ele é maior. Caso seja, os valores maiores andam 1 casa para a direita para que, espaço seja aberto para o novo elemento. Após a criação do espaço, ele é realocado dentro do sub-conjunto ordenado (linha 11) e o contador do primeiro loop é incrementado, ou seja, o marcador anda 1 passo para a direita.

Tudo o que foi explicado nos parágrafos anteriores é exemplificado de forma animada pela figura 3 abaixo.

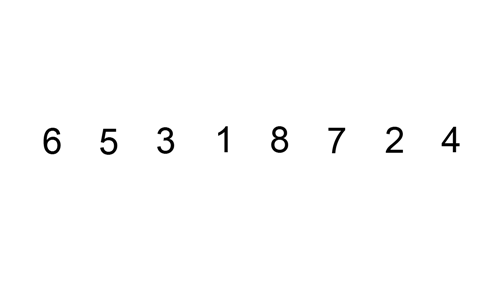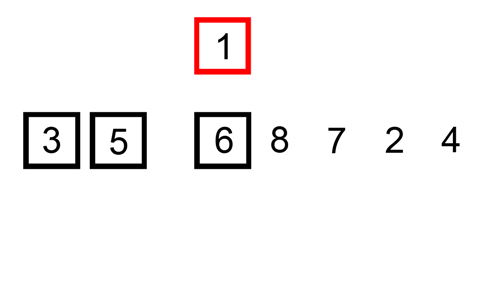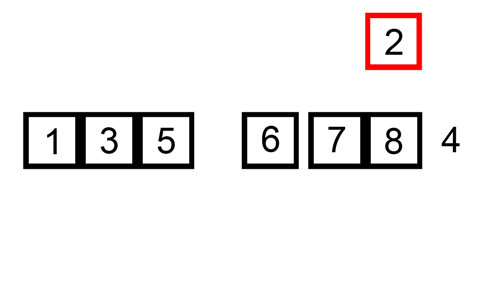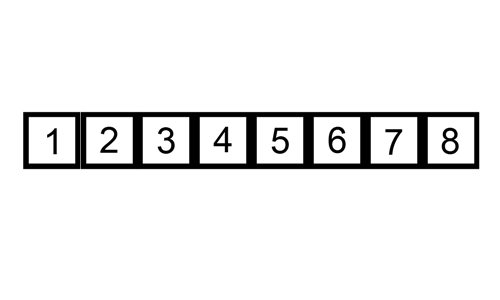Figura 3 - Gif animado representando funcionamento do algoritmo

Pronto !! Isso é tudo o que precisamos ! Vamos fazer alguns testes ????

Figura 4 - Resultados do primeiro teste

Os resultados do primeiro teste podem ser visto na figura 4. É possível concluir que o algoritmo possui um ótimo tempo de processamento para grandes conjuntos desordenados visto que, para 10000 elementos teve tempo de 11 milissegundos. Tal medida já deixou seu primo, o algoritmo BubbleSort, comendo poeira pois, para o mesmo conjunto ele levou 82 milissegundos.

Nosso segundo teste será ordenar dois conjuntos, ambos com com 1 milhão de números, mas um parcialmente ordenado e o outro totalmente desordenado, e após executados, comparar seus tempos de execução. Seguem resultados:

Completamente desordenado: 106394 milli ≅ 106,394 s ≅ 1,773 m
Parcialmente ordenado: 101051 milli ≅ 101,051 s ≅ 1,684 m

Os tempos tendem a se distanciar conforme a quantidade de elementos parcialmente ordenados aumenta. Nosso sub-conjunto ordenado possui 1000 elementos, ou seja, 0,1% do total.

Pronto !!! Adicionamos mais um item ao nosso canivete de algoritmos !!

Figura 5 - Chegamos ao fim

Link no github: https://github.com/PrecisoEstudarSempre/InsertionSort.git

Dúvidas !? Sugestões ?! Críticas ou elogios ?!

Deixe aí nos comentários, me mande um e-mail ou, na nossa página do facebook.

E-mail: precisoestudarsempre@gmail.com

Facebook: https://www.facebook.com/precisoestudarsempre/

Referências:
Estruturas de dados e algoritmos em Java - Lafore, Robert

Imagens:
Figura 5 - http://youpix.virgula.uol.com.br/wp-content/uploads/2012/03/para-nossa-alegria-meme.jpg
Figura 3 - https://upload.wikimedia.org/wikipedia/commons/9/9c/Insertion-sort-example.gif
Gif insertion sort - https://upload.wikimedia.org/wikipedia/commons/9/9c/Insertion-sort-example.gif