Olá ! Meu nome é João Paulo Maida e bem-vindos ao blog Preciso Estudar Sempre.
Você já pensou em alguma vez fazer uma daquelas viagens como mochileiro que você sai sem rumo de casa, só com mochila e dinheiro para a passagem do ônibus ? Seu destino final você decide a cada parada. Hoje você pode estar saindo do Rio de Janeiro e amanhã estar amanhecendo em alguma cidade do interior de Minas Gerais. A partir de lá você pode decidir ir para São Paulo, e de lá para o Mato Grosso. Em cada cidade que você pára, avalia quais podem ser seus destinos e quais são os mais baratos. Até porque para este tipo de viagem a grana é sempre curta.
Devo admitir que este tipo de aventura sempre foi um sonho para mim, mas acho que dificilmente um dia irei realizá-lo. Se você um dia já se aventurou de tal forma ou pensa em se aventurar, sabe que seria interessante ter uma relação das conexões das cidades baseadas em seus custos de transporte onde esses são baseados em suas distâncias, exemplo: ir do RJ para SP custa R$ 80, do RJ para MG custa R$60, de MG para MT custa R$30 e por aí vai. Com essa relação em mãos fica fácil decidir qual caminho tomar gastando pouco com passagem. Seria um sonho, não ?
Para nossa alegria e felicidade, este sonho sim é possível atingir. Mais uma vez a teoria dos grafos chega para salvar o dia com um algoritmo que nos dá exatamente a resposta que estamos procurando. Apresento o algoritmo de Dijkstra. A criação de Edsger Dijkstra é baseada na representação da matriz de adjacência de um grafo e não somente encontra o caminho mais curto a partir de um nó especificado até outro, como também os caminhos mais curtos do mesmo nó especificado até os outros (LAFORE, ROBERT).
Imaginemos a nossa viagem aventureira representada pela Figura 1 e não se prenda a detalhes de geografia.
 |
| Figura 1 - Mapa das cidades |
Você está partindo do Rio de Janeiro e quer saber quais são os caminhos mais baratos para as próximas cidades, para assim chegar ao seu destino final pelo melhor caminho. Você sabe que em cada cidade que pára existe um agente da empresa de ônibus e que ele pode te informar os trajetos e tarifas. Então, você pega seu bloquinho (todo bom viajante deve ter um) e faz uma tabelinha com essa relação para que no final você tenha todas as informações “mastigadas”.
 |
| Tabela 1 - Tabela das viagens mais baratas |
É aí que entra o algoritmo de Dijkstra. Ele pega o seu grafo, analisa, e como resultado gera uma árvore. Esta árvore segue os conceitos básicos de uma árvore mas não é como uma árvore geradora mínima, a qual já vimos (clique aqui). Ela é diferente porque é montada levando em conta o somatório dos pesos a partir do nó inicial.
Abaixo estão relacionadas as etapas do algoritmo. Os detalhes de cada uma serão vistos mais à frente. Com o entendimento dessas etapas, entender o algoritmo em Java fica muito mais fácil.
Etapas do algoritmo:
- Lembra da tabelinha da relação dos caminhos mais baratos ? Aqui ela toma a forma de um array, onde seu tamanho reflete a quantidade de vértices do grafo, cada posição representa um vértice e inicialmente é preenchido por completo com um valor muito grande (veremos o motivo disso mais à frente) que chamaremos de INFINITY. Chamaremos este array de array de menor caminho.
- Após montado, o nó inicial, ou seja, nosso ponto de partida é analisado. São adicionados no array de menor caminho somente os vértices que são adjacentes ao nó inicial. Essa adição tem a forma de um objeto com informações sobre o vértice antecessor ao vértice analisado e o custo para chegar até ele. É necessário ter informações sobre o antecessor pois precisamos saber como chegamos ali (entenderemos esse ponto melhor a frente). Porque é assumido que estes vértices representam os melhores caminhos a partir do vértice inicial e podem ser inseridos no array de menor caminho ? A resposta é óbvia. Se os nós que são inseridos no array são aqueles adjacentes ao nó inicial, logo não existe nada que separe-os e assim se tornam os melhores custos neste trajeto. É importante citar que essas adições são feitas por cima dos valores que já existem em uma determinada posição do array.
- Lembra que o resultado do algoritmo de Dijkstra é uma árvore ? Então, já podemos adicionar o primeiro nó (início) na árvore.
- A partir dos nós restantes, verificamos 1 por 1 para averiguar qual tem o menor custo a partir do início.
- Caso não haja nenhum é porque o nó inicial não tem conexões, ou seja, é inatingível ou todos já estão na árvore. Caso contrário, o nó com menor custo (adjacente ao inicial neste caso) é selecionado.
- Uma vez selecionado, é adicionado na árvore e o array de menores caminhos é atualizado.
- A atualização tem forma parecida com a adição citada no passo 2, ou seja, a mesma estrutura de objeto é citado. Consiste em analisar se o somatório de valores do início até o nó selecionado é menor que o valor já registrado. Isto deve ser feito por causa do passo 2.
- Após esses passos terminados, o array de menor caminho está finalizado.
 |
| Tabela 2 -Tabela de viagens mais baratas preenchida |
Através da Tabela 2 fica claro porque precisamos da informação do antecessor ? Com ela em mãos conseguimos refazer todo o caminho feito desde do nó inicial, ou seja, agora eu sei que o melhor caminho para a cidade de Bonito no estado do Mato Grosso do Sul é através de Ribeirão Preto em São Paulo e que o melhor caminho para este é via São Paulo capital, e para este o melhor é caminho é vir diretamente de Rio de Janeiro capital. Tudo mais claro agora não !?
Agora veremos a implementação desse algoritmo em Java e como já é de costume, é necessário dizer que é possível implementar este algoritmo em qualquer linguagem de programação. A linguagem Java foi escolhida somente por uma questão de afinidade.
O código abaixo é um dos mais difíceis já mostrados aqui no blog, mas não se espante que com calma tudo fica fácil. Não mostrarei o código inteiro aqui porque tal tornará a leitura complicada, visto que o que realmente importa são as três funções chave as quais compõem o algoritmo de Dijkstra.
findAllShortestPaths()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | public void findAllShortestPaths(){ int startTree = 0; vertexList[startTree].setIsInTree(true); //adiciono o primeiro vértice do grafo na árvore nTree = 1; //mudo o contador porque acabei de adicionar um nó na árvore for (int i=0; i<nVerts; i++) { //inicializo o array de menores caminhos com as distâncias int distance = adjMat[startTree][i]; //das adjacências do primeiro vértice shortestPathArray[i] = new ShortestPathObject(startTree, distance); } while (nTree < nVerts) { //até todos os nós estarem na árvore int shortestVertex = getMin(); //seleciona o vértice que tem o valor mínimo, essa função provê int shortestDistance = shortestPathArray[shortestVertex].getDistance(); //a direção que o algoritmo vai seguir if(shortestDistance == INFINITY){ //se todos forem infinito ou todos na árvore System.out.println("There are unreachable vertices"); break; } else { currentVert = shortestVertex; startToCurrent = shortestDistance; } vertexList[currentVert].setIsInTree(true); //coloca o vértice atual na árvore nTree++; //mais um nó entrou na árvore updateShortestPathArray(); //atualizo os valores mínimos } displayPaths(); //exibo todos os nós nTree = 0; //limpa a ávore for (int i=0; i<nVerts; i++) { vertexList[i].setIsInTree(false); } } |
Aqui é onde acontece toda a mágica. Como existem muitos detalhes que devem ser vistos, esta função divide essa responsabilidade com duas outras funções: getMin() e updateShortestPathArray(). Tentei deixar o código o mais explicado possível através de comentários, nomes de variáveis e métodos. Por causa disso não me estenderei em explicações aqui.
getMin() e updateShortestPathArray()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | private int getMin(){ int shortestDistance = INFINITY; int shortestVertex = 0; for (int i=1; i<nVerts; i++) { //passo por todos os nós if (!vertexList[i].isInTree() && shortestPathArray[i].getDistance() < shortestDistance) { //analiso se o nó já está na árvore e se a distância dele shortestDistance = shortestPathArray[i].getDistance(); //é a menor. Se for, atualizo as variáveis shortestVertex = i; } } return shortestVertex; } private void updateShortestPathArray(){ int column = 1; while (column < nVerts) { //percorre todas as colunas da "tabelinha" if (vertexList[column].isInTree()) { //se a coluna da "tabelinha" já estiver na árvore não há column++; //de atualizar sua entrada no array de valores mínimos continue; } int currentToTarget = adjMat[currentVert][column]; //variável que guarda o valor da distância do nó atual(RJ) até um nó de destino que não está na árvore, nem sempre esse vértice de destino tem uma conexão de fato int startToTarget = startToCurrent + currentToTarget; //variável que guarda a distância total do início até o destino int shortestDistance = shortestPathArray[column].getDistance(); //recupera o valor do array de valores mínimos if (startToTarget < shortestDistance) { //essa comparação é essencial pois se não há uma conexão de fato entre dois vértices, a soma total será INFINITY + algum valor de aresta e este é menor que somente INFINITY, logo não há necessidade de atualização nesse caso. shortestPathArray[column].setParentVert(currentVert); //caso a soma seja de valores que realmente possuem conexão (RJ-SP-RP-BN) ela será menor que INFINITY e logo há porque atualizar shortestPathArray[column].setDistance(startToTarget); } column++; } } |
Entender o que essas funções fazem é essencial para um entendimento total da implementação do algoritmo. Elas possuem tanta importância quanto a função findAllShortestPaths(). Basicamente, a função getMin() decide a direção de exploração no grafo escolhendo o nó com o melhor (menor no nosso caso) custo possível que ainda não está na árvore. Outro detalhe importante é que a ação de adicionar um vértice do grafo em uma árvore apartada é o fator determinante para que aquele vértice não seja mais analisado pelo algoritmo.
A função updateShortestPathArray() atua na atualização do array de menores caminhos e avalia se o custo de um trajeto inteiro vale a pena ou não de ser computado como ou não como um melhor caminho. Sem essa função não teríamos os resultados que tanto desejamos. No fim das contas, o que esperamos é a Tabela 2, já mostrada acima, e a Figura 3 que representa a árvore gerada pelo algoritmo.
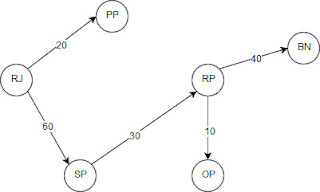 |
| Figura 3 - Árvore montada pelo algoritmo de Dijkstra |
Até a próxima minha boa gente ! 😘
Leia nossa postagem anterior: Você já parou para pensar sobre controle transacional ?
Download do código-fonte
Github: https://github.com/PrecisoEstudarSempre/Graphs.git
Dúvidas !? Sugestões ?! Críticas ou elogios ?!
Deixe aí nos comentários, envie um e-mail ou uma mensagem na nossa página do Facebook.
E-mail: precisoestudarsempre@gmail.com
Facebook: https://www.facebook.com/precisoestudarsempre/
Canal Preciso Estudar Sempre: https://www.youtube.com/channel/UCUoW8dS38rXr0a5jWU57etA
Referências
LAFORE, ROBERT; Estruturas de Dados e Algoritmos em Java; 2004

Nenhum comentário:
Postar um comentário