Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.
Até este momento já vimos bastante coisa sobre grafos. Estudamos seus conceitos mais fundamentais, tipos de buscas, árvores geradoras mínimas e por último, orientação. A orientação se torna um grande divisor de águas quando o assunto é grafos. Isto acontece pelo simples fato de que a adição de direção nas arestas muda completamente as regras do jogo. Se antes era possível iniciar um trajeto em um determinado ponto e terminar em outro, agora não é mais, e tal fato se torna uma pergunta. Como determinar todos os caminhos possíveis de um grafo ? Quais são as aplicações disso no mundo real ?
Bem, a segunda pergunta é fácil de responder. Basta pensar em um aeroporto, como o aeroporto do Galeão no Rio de Janeiro, e tentar determinar quais viagens são possíveis de fazer a partir dele. Cada aeroporto representaria um nó e cada trajeto direto (sem escalas) possível uma aresta. Logo, se existe uma viagem que parte do Galeão e vai para Frankfurt na Alemanha, teremos dois nós G e F (representados pelas primeiras letras dos aeroportos) ligados por uma seta iniciando em G e indo para F. Em seguida, se somente a partir de Frankfurt é possível ir para Varsóvia, na Polônia, então será necessário realizar o trajeto Galeão -> Frankfurt -> Varsóvia. Não existe outro caminho possível.
Para o nossa primeira pergunta o que era problema se torna trivial, pois estamos analisando um exemplo muito pequeno mas imagine um cenário real, onde você pode ir para qualquer lugar do mundo e muitas vezes só existem caminhos de ida e não de volta. Acredito que as coisas se compliquem um pouco. Então determinar um procedimento capaz de realizar esse mapeamento completo se torna crucial.
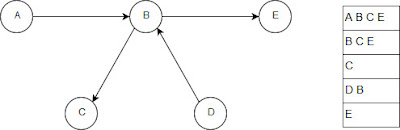 |
| Figura 1 - Grafo orientado G com sua tabela de conectividade |
Analisando rapidamente a tabela é possível concluir que isto é uma inverdade, e somente é possível chegar a essa conclusão pois vimos letra após letra da sequência que começa com A. Tal processo é custoso visto que leva tempo O(N), onde N é o número médio de nós alcançados a partir de um determinado nó. Mas, conforme citado acima, procuramos uma forma direta de obter essa informação, procuramos uma forma que leve tempo O(1) (LAFORE, ROBERT).
Tal almejada forma é o algoritmo de Warshall e sua ideia é extremamente simples. Ele utiliza uma estrutura já conhecida, a matriz de adjacência, e insere novas informações nela, a fim de torná-la mais rápida. A matriz melhorada gera um grafo chamado de fechamento transitivo do grafo original (LAFORE, ROBERT).
Para entendermos como funciona o algoritmo, antes precisamos tomar conhecimento da matriz de adjacência do grafo atual.
 |
| Figura 2 - Matriz de adjacência do grafo G |
LEMBRETE: As linhas representam as origens de uma aresta e as colunas os fins, ou seja, se na célula AB existe o número 1 logo existe uma aresta de A para B.
----------------------------------------------------------------------------------------------------------------
O algoritmo deve percorrer todas as células da matriz. Caso encontre 1 em alguma célula, ele saberá que ali existe uma aresta. Para cada aresta encontrada ele deve percorrer todas as células da coluna correspondente à sua linha, ou seja, se foi encontrado 1 na célula AB, a coluna A deverá ser percorrida completamente. Caso nesta coluna exista algum 1, ele saberá que existe uma aresta chegando naquele nó, onde a origem será a linha dessa célula. Neste exato momento é concluído que existem dois caminhos que partilham um mesmo nó. Então, se existe tal caminho ele pode ser “encurtado” em um caminho só, logo um 1 é adicionado na célula correspondente a esse caminho. Confuso ? Nem um pouco. A Figura 3 mostra como o processo funciona.
 | |
| Figura 3 - Funcionamento do algoritmo de Warshall |
A verificação começa e a aresta B -> C é descoberta. A coluna B é verificada e a aresta A -> B é encontrada, logo o nó B é comum as duas arestas e através dele é possível conectar A à C. Por fim, a célula AC é marcada com 1 para representar que existe uma aresta que liga esses dois nós. Este procedimento é repetido para todos os nós das linhas da matriz. Quando não houver mais linhas para serem processadas, o algoritmo chegou ao fim.
Abaixo apresento uma implementação feita em Java para este algoritmo. Como já é de costume é importante deixar bem claro que escolhi Java por uma questão de afinidade e nada impede que você escolha uma linguagem de seu gosto. Nosso foco aqui não é realizar as melhores práticas da linguagem, mas sim aprender como o algoritmo funciona.
Graph.java
O algoritmo é bem simples visto que são três laços de repetição com algumas condicionais. O primeiro laço consiste na varredura das linhas da matriz, o segundo das colunas. Caso haja uma aresta, a procura na coluna correspondente é feita no terceiro laço. Se todas as correspondências forem encontradas o novo caminho é gravado na matriz. Todo este procedimento é repetido para todas as linhas da matriz fazendo com que o algoritmo chegue ao fim e torne o acesso à caminhos de um grafo O(1).
WarshallAlgorithm.java
Esta classe é apenas uma classe cliente, sua única responsabilidade é criar grafos, adicionar arestas e vértices, e executar o algoritmo de Warshall. Exibir o fechamento transitivo do grafo original e checar possíveis caminhos também são operações realizadas aqui.
A partir dessa postagem entraremos em uma outra classe de grafos, os grafos ponderados. Aqui veremos que é possível atribuir pesos para as arestas e ver qual é o melhor caminho a ser feito, assim como os programas de GPS fazem. Mais um passo no longo caminho do entendimento desta extraordinária teoria foi dado.
Até a próxima minha boa gente ! 😘
Leia nossa postagem anterior: A orientação em grafos - Grafos
Download do código-fonte
Link do repositório GitHub: https://github.com/PrecisoEstudarSempre/Graphs.git
Dúvidas !? Sugestões ?! Críticas ou elogios ?!
Deixe aí nos comentários, envie um e-mail ou uma mensagem na nossa página do Facebook.
E-mail: precisoestudarsempre@gmail.com
Facebook: https://www.facebook.com/precisoestudarsempre/
Canal Preciso Estudar Sempre: https://www.youtube.com/channel/UCUoW8dS38rXr0a5jWU57etA
Referências
LAFORE, ROBERT; Estruturas de Dados e Algoritmos em Java; 2004

10 comentários:
Muito bom !!!
Muito obrigado Marlysson. Fique sempre à vontade para comentar mais e dar sua opinião nas nossas postagens. Aqui é o espaço onde você deve se sentir confortável para trocar idéias, criticar ou elogiar.
Muito obrigado por tudo.
Show!! Acompanharei teu blog .. conteúdo muito bom..
Também estou vendo essa parte de Estrutura de dados , mas até agora vendo mais web..
Já viu algo relacionado à hashes?
Só sugestão : Já pensou em utilizar algo como o jekyll?
Tenho um blog usando pelican .. e fica muito bom..
Muito obrigado mais uma vez.
Em relação à hashes já escrevi sim. Dê uma olhada.
https://precisoestudarsempre.blogspot.com.br/2015/07/conheca-verdade-tabelas-hashsem-colisao.html
Em relação a sua sugestão, não conheço nenhuma dessas duas ferramentas. O que são ?
São geradores de conteúdo, tipo um cms( mas não tão robusto ) ,eles nos dão só o necessário para focarmos no conteúdo e eles nos dão temas mais customizáveis e ficam bem legais com o propósito de servir conteúdo como blog.. podendo até hospedar no Github.
Ahh tem também o Medium , interessante também..
E como eu faria para migrar o conteúdo já desenvolvido nessa plataforma ?
Para o jekyll há essa forma:
http://import.jekyllrb.com/docs/blogger/
Já para o pelican acredito que usando essa funcione:
http://docs.getpelican.com/en/stable/importer.html
A do pelican usa um feed rss do conteúdo gerado ( acredito que dê pra importar também )..
Eu vi os links que você mandou e gostei muito dos dois, mas ainda tenho algumas dúvidas.
Ambas as ferramentas são plataforma para blogs né ?! Então neles eu vou poder escrever meu conteúdo e publicar ?
Sim sim , tenho um exemplo:
Uso o pelican para esse blog:
marlysson.github.io
Aí escrevo em markdown e gero o html , e uso um template que já tem toda a estrutura , escrevo só o conteúdo depois gero ele no template .. depois só fazer deploy no github.
Postar um comentário