Busca em largura - Grafos

Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.

Na nossa última postagem abordamos uma das formas de se realizar uma busca em um grafo, a busca em profundidade. Caso você não tenha lido, clique aqui. Mas, se você for um total iniciante no assunto, recomendo que você comece lendo a primeira postagem dessa nova série, clicando aqui.

Já informo de antemão que utilizarei a linguagem de programação Java para a construção das implementações dos algoritmos e que nada impede que você utilize uma outra versão do Java diferente da minha ou, até uma outra linguagem. Agora, sem mais delongas, vamos ao assunto.

A necessidade e as restrições que envolvem este assunto são as mesmas que envolviam o assunto da postagem anterior. Dado um grafo G desconhecido, quais nós são possíveis de atingir a partir de um determinado nó N ? Esta pergunta, obviamente, já foi respondida, mas aqui veremos uma outra forma de respondê-la.

Analisemos o grafo mostrado na Figura 1.

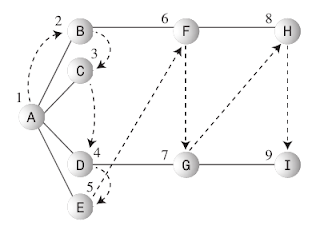Figura 1 - Grafo de exemplo

Assim como já foi discutido previamente, é necessário que um ponto de partida seja escolhido, pois o grafo analisado é desconhecido de primeira mão, estamos às cegas. Só teremos o conhecimento de um ponto inicial, o nó A no nosso caso. Tal condição não somente viabiliza a pergunta feita acima, mas como nos deixa à frente de grandes problemas, como: O que fazer ? Qual nó adjacente visitar primeiro ?

Ao contrário de sua irmã, a busca em largura não visita a fundo todo um caminho de arestas até chegar em um ponto que não consiga ir mais adiante, ela se comporta de uma forma completamente diferente. Ela visita todos os nós adjacentes ao nó inicial e apenas então vai mais adiante. A estrutura que serve como alicerce para tudo isso é uma fila do tipo FIFO, pois é ela que vai registrar qual é o caminho atual percorrido. Caso você não seja conhecedor de tal estrutura, recomendo fortemente o estudo dela antes de continuar a leitura deste post e peço desculpas por não deixar uma referência de post do próprio blog sobre o assunto. Não faço isso, pois ainda não abordei esse tema.😞

Imagine o seguinte: uma pedra cai na água de uma calma lagoa (LAFORE, ROBERT). Quando a pedra entra em contato com a água, ela cria ondas que se espalham de forma igual por toda a superfície criando assim um fenômeno homogêneo. Tal característica se repete nas buscas em largura, ou seja, os nós são percorridos de uma forma igual em relação às suas adjacências. Isto significa que todos os nós que estão a uma aresta de distância do ponto inicial são encontrados primeiro, então todos os nós que estão a duas arestas de distância são encontrados em seguida, e etc. Tal característica será útil se você estiver tentando encontrar o caminho mais curto do nó inicial até um determinado nó (LAFORE, ROBERT).

Para uma execução organizada e procedural, três regras foram criadas. São elas:

Regra 1
Visite o próximo nó não visitado, se existir, que seja adjacente ao nó atual, marque-o e insira-o na fila (LAFORE, ROBERT).

Lembre que nosso ponto de partida é o nó A, já temos conhecimento sobre ele, logo nenhum processamento a mais é necessário. Tal fato nos permite a executar a regra 1, o que nos leva ao nó B. Após isso, devemos verificar se A não possui nenhum outro nó adjacente não visitado ainda, e então descobrimos C, D e E. Para estes três últimos nós, a regra 1 deve ser aplicada. Agora na fila temos: B C D E.

Após executar a regra 1 para todos os nós adjacentes à A, não teremos mais nós adjacentes não visitados. Então, o que fazer ? Para esta necessidade surge a regra 2.

Regra 2
Se você não puder executar a Regra 1 porque não há mais nó não visitado, remova um nó da fila e torne-o o nó atual (LAFORE, ROBERT).

Removendo um nó da fila teremos B, mas porque não E ? Isto acontece devido ao tipo de fila que estamos utilizando. A sigla FIFO significa first-in-first-out, ou seja, o primeiro que entra é o primeiro que sai, assim como na fila de um banco. Logo, filas que usem esse tipo de esquema de organização de itens terão este comportamento, e este é o nosso caso.

Voltando à nossa linha de raciocínio, remover um nó da fila resultará no nó B, e este é o nosso nó atual. Uma nova execução da regra 2 se faz necessária, mas agora é possível executar a regra 1 pois o nó atual possui nós adjacentes não visitados. Isto fará com que F entre na fila.

C sai da fila, não possui adjacências. Devemos remover o próximo pois a regra 1 não consegue ser satisfeita, logo removemos D da fila. A partir deste, enfileiramos G e concluímos que assim como C, o nó E sai da fila e não possui adjacências.

A interação entre a regra 1 e a regra 2 recria o fenômeno de onda citado anteriormente, pois as adjacências de F e G só serão exploradas totalmente quando todos os nós que estão no mesmo “nível” de seus pais forem exploradas primeiro.

A regra 2 é executada em F, menos um na fila e em seguida H é enfileirado pela regra 1. O mesmo acontece para I quando G é desenfileirado. Execuções contínuas da regra 2 em conjunto da 1 resultarão em uma fila vazia, o que nos leva à regra 3.

Regra 3
Se não puder executar a Regra 2 é porque a fila está vazia, terminou (LAFORE, ROBERT).

Visto que houveram muitas movimentações na fila durante a execução das regras, a Tabela 1 mostra de forma detalhada o passo a passo de todas as operações realizadas.

Evento	Fila
Vá para A
Vá para B	B
Vá para C	BC
Vá para D	BCD
Vá para E	BCDE
Remova B	CDE
Vá para F	CDEF
Remova C	DEF
Remova D	EF
Vá para G	EFG
Remova E	FG
Remova F	G
Vá para H	GH
Remova G	H
Vá para I	HI
Remova H	I
Remova I
Terminado

Se você leu o post anterior sobre busca em profundidade notará que as diferenças são grandes. Compare como as duas abordagens funcionam e deixe sua opinião nos comentários.👍

Visto que já conhecemos toda a teoria necessária para entender e executar uma busca em largura, podemos a partir daí transcrever este algoritmo para um programa Java.

Este método executa as três regras descritas acima de uma forma bem simples. Ele inicia adicionando o primeiro nó do grafo, o ponto de partida, na fila, e partir daí verifica repetidamente se a fila não está vazia. Caso negativo a busca chegou ao fim pois não existem mais nós para analisar, mas caso contrário, ainda existem nós não explorados e os processos descritos nas regra 1 e 2 são executados.

É possível notar que um método auxiliar é utilizado para verificar as adjacências de um determinado nó. Por tal motivo, o segundo laço de repetição se faz necessário pois um nó pode ter N adjacências.

O último laço de repetição utilizado tem a finalidade de somente resetar a flag de visitação dos nós para que buscas futuras possam ser executadas sem problemas.

O método getAdjUnvisitedVertex(vertexIndex) é responsável para um determinado nó obter seus nós adjacentes não visitados, conforme citado acima. Sua implementação é simples e tem apoio da matriz de adjacência e da flag de visitação para a recuperação da informação desejada. Caso encontre, retorna a posição deste nó no array de nós, caso contrário, retorna -1 simbolizando que não encontrou nada.

Ambos os métodos fazem parte de uma classe que foi criada em postagens passadas. Logo, os detalhes que já foram incorporados não serão abordados aqui. Para que você tenha uma visão geral de tudo feito até agora, faça o download do projeto usando o link do repositório no fim do post.

A classe acima é somente utilitária. Sua única responsabilidade é criar e montar um grafo para depois executar a busca em largura nele. O resultado esperado de sua execução é o caminho percorrido pelo algoritmo de busca.

Esta postagem é somente mais uma que compõe a grande série de assuntos envolvendo a teoria dos grafos. Em publicações futuras veremos árvores geradoras mínimas, o algoritmo de Warshall e etc.

Até a próxima minha boa gente ! 😘

Leia nossa última postagem sobre grafos: Busca em profundidade - Grafos

Download do código-fonte
Link do repositório GitHub: https://github.com/PrecisoEstudarSempre/Graphs.git

Dúvidas !? Sugestões ?! Críticas ou elogios ?!

Deixe aí nos comentários, envie um e-mail ou uma mensagem na nossa página do Facebook.

E-mail: precisoestudarsempre@gmail.com
Facebook: https://www.facebook.com/precisoestudarsempre/
Canal Preciso Estudar Sempre: https://www.youtube.com/channel/UCUoW8dS38rXr0a5jWU57etA

Referências

LAFORE, ROBERT; Estruturas de Dados e Algoritmos em Java; 2004