Árvore binária - Implementação em Java

Olá amados leitores. Hoje iremos estudar um tema muito interessante nas estruturas de dados, as árvores binárias. Para você que já conhece toda a parte teórica da coisa e só quer um exemplo prático, você pode clicar aqui e baixar um projeto pronto.

Ahhhhhhhhhhhhhhhhh, antes que alguém me pergunte: "Ainnn João, você vai falar sobre balanceamento ?"

Eu já respondo: "Não vou falar porque senão o post vai ficar extremamente extenso". Você vai ter que correr por fora amigo.

Vamos começar então ?!

Você sabe o que é uma árvore binária ? 

Não !?

Tudo bem amigo, vamos facilitar um pouco mais a pergunta. To pegando pesado !

Você sabe o que é um árvore (não me refiro a planta) ?

Também não !?

Bem, então, senta aí que lá vem história. Pegue seu café e acenda seu cigarro. Uma árvore, não é nada mais nada menos que, um grafo acíclico. Mas aí você me pergunta: O que é um grafo ?

Vamos descer mais um degrau. Segundo à Wikipedia, a teoria dos grafos é um ramo da matemática que estuda as relações entre os objetos de um determinado conjunto. Para representar tais relações, são usados estruturas chamadas grafos, G(V,A) onde, G é um conjunto de vértices e arestas. Os vértices são um conjunto não vazio dos vértices do grafo. As arestas são um conjunto de pares não ordenados de V. Vamos ao exemplo.

Figura 1 - http://upload.wikimedia.org/wikipedia/commons/thumb/2/24/Tree_graph.svg/162px-Tree_graph.svg.png

Acima, temos o grafo G que é composto por V={1,2,3,4,5,6} e A={{1,4},{2,4},{4,3},{4,5},{5,6}}. Depois de toda essa explicação, você deve estar se perguntando: Para que esta porcaria serve ? Quem usa isso ?

Agora você vai ficar surpreso. Pesquise sobre o problema das sete pontes de Königsberg. Não irei falar sobre o problema das pontes aqui porque não é esse o nosso foco.

Lembra que no início do post, eu falei que uma árvore é um grafo acíclico ? Então, um grafo acíclico é aquele que não faz ciclos, ou seja, se no nosso exemplo acima, o vértice 1 estivesse ligado ao vértice 2, o grafo G não seria uma árvore pois, existiria um ciclo, 1 - 2 - 4.

Agora que, já sabemos o que é um grafo e o que é uma árvore. Vamos falar de suas propriedades:

• O primeiro nó de uma árvore é o nó raiz.
• Nó folha é todo nó que não possui conexões.
• Em uma árvore existe 1 e somente 1 caminho que liga um nó ao outro.
• Dado um determinado vértice, cada "filho" seu é a "raíz" de uma nova "sub-árvore".
• Grau de um vértice é o número de sub-árvores do vértice.
• Altura da árvore é o comprimento do caminho mais longo da raiz até uma das suas folhas.
• O nível de um nó é o número de nós no caminho entre o vértice e a raiz.

Precisamos saber o que é uma árvore binária. Afinal de contas, estamos aqui para isso. As árvores binárias são um tipo de árvore onde, cada um de seus vértices pode possuir no máximo duas sub-árvores. O grau (número de filhos) de cada vértice pode ser 0, 1 ou 2.

Figura 2

Acima, temos um exemplo de árvore binária. Neste momento, não se preocupe em entender como os valores foram gravados ali. Veremos isto adiante. Vamos a melhor parte do post, vamos implementar !!!

Usaremos uma lista encadeada para construir nossa árvore por questões de performance. Se você não sabe o que é uma lista encadeada, eu recomendo que você dê uma olhada nesse post:

http://precisoestudarsempre.blogspot.com.br/2014/12/listas-encadeadas-em-java.html

Vamos primeiro criar métodos para retornar se a árvore está vazia ou não, a quantidade de nós da árvore, altura da árvore e um método que imprima todos os valores da árvore. A forma que a árvore é percorrida é em pós-ordem pois, dessa forma é garantido que irei percorrer todos os filhos de um nó primeiro e só depois irei acessar o nó pai. Dessa forma, realizo as operações na árvore de um jeito mais seguro.

Crie as seguintes classes:

package pkg;



public class Node {

    private Integer valor;

    private Node noEsquerda;

    private Node noDireita;  

    public Node() { }

  

   public Node(Integer valor) {

        super();

        this.valor = valor;

    }

    public Integer getValor() {

        return valor;

    }

    public void setValor(Integer valor) {

        this.valor = valor;

    }

    public Node getNoEsquerda() {

        return noEsquerda;

    }

    public void setNoEsquerda(Node noEsquerda) {

        this.noEsquerda = noEsquerda;

    }

  public Node getNoDireita() {

        return noDireita;

    }

    public void setNoDireita(Node noDireita) {

        this.noDireita = noDireita;

    }



    @Override

    public String toString() {

        return "Node [valor=" + valor + "]";

    }    

}

package pkg;

public class BinaryTree {
    private Node root;

    public boolean isEmpty(){
        if(root == null){
            return true;
        }
        return false;
    }
    
    public int getAltura(){
        return getAltura(this.root);
    }
    
    private int getAltura(Node root){
        if(root == null){
            return 0;
        }
        int altEsq = getAltura(root.getNoEsquerda());
        int altDir = getAltura(root.getNoDireita());
        if(altEsq > altDir){
            return altEsq + 1;
        } else {
            return altDir + 1;
        }
    }
    
    public int getQtdNode(){
        return getQtdNode(root);
    }
    
    private int getQtdNode(Node root){
        if(root == null){
            return 0;
        }
        int qtdNodeEsq = getQtdNode(root.getNoEsquerda());
        int qtdNodeDireita = getQtdNode(root.getNoDireita());
        return qtdNodeEsq + qtdNodeDireita + 1;
    }
    
    public void imprimirArvore(){
        if(this.root == null)
            System.out.println("Árvore vazia");
        else
            imprimirArvore(this.root);
    }
    
    private void imprimirArvore(Node node){
        if(node.getNoEsquerda() != null){
            imprimirArvore(node.getNoEsquerda());
        }
        if (node.getNoDireita() != null){
            imprimirArvore(node.getNoDireita());
        }
        System.out.println("Nó: " + node.getValor());
    }
    
    public void inserir(int valor){
        inserir(this.root, valor);
    }
    
    public void inserir(Node node, int valor) {
        if(this.root == null){
            this.root = new Node(valor);
        } else {
            if (valor < node.getValor()) {
                if (node.getNoEsquerda() != null) { 
                    inserir(node.getNoEsquerda(), valor); 
                } else { 
                    //Se nodo esquerdo vazio insere o novo no aqui 
                    node.setNoEsquerda(new Node(valor)); 
                } 
                //Verifica se o valor a ser inserido é maior que o no corrente da árvore, se sim vai para subarvore direita 
            } else if (valor > node.getValor()) { 
                //Se tiver elemento no no direito continua a busca 
                if (node.getNoDireita() != null) { 
                    inserir(node.getNoDireita(), valor); 
                } else {
                    //Se nodo direito vazio insere o novo no aqui 
                    node.setNoDireita(new Node(valor)); 
                } 
            }
        }
    }
    
    public Node remover(int valor) throws Exception{
        return remover(this.root, valor);
    }
    
    private Node remover(Node node, int valor) throws Exception{
        if(this.root == null){
            throw new Exception("Árvore vazia");
        } else {            
            if(valor < node.getValor()){
                node.setNoEsquerda(remover(node.getNoEsquerda(), valor));
            } else if(valor > node.getValor()){
                node.setNoDireita(remover(node.getNoDireita(), valor));
            } else if (node.getNoEsquerda() != null && node.getNoDireita() != null) {
                /*2 filhos*/  
                System.out.println("  Removeu No " + node.getValor());
                node.setValor(encontraMinimo(node.getNoDireita()).getValor());
                node.setNoDireita(removeMinimo(node.getNoDireita()));
            } else {  
                System.out.println("  Removeu No " + node.getValor());  
                node = (node.getNoEsquerda() != null) ? node.getNoEsquerda() : node.getNoDireita();  
            }  
            return node;
        }
    }
    
    private Node removeMinimo(Node node) {  
        if (node == null) {  
            System.out.println("  ERRO ");  
        } else if (node.getNoEsquerda() != null) {  
            node.setNoEsquerda(removeMinimo(node.getNoEsquerda()));  
            return node;  
        } else {  
            return node.getNoDireita();  
        }  
        return null;  
    }  
  
    private Node encontraMinimo(Node node) {  
        if (node != null) {  
            while (node.getNoEsquerda() != null) {  
                node = node.getNoEsquerda();  
            }  
        }  
        return node;  
    }
}

Agora que você já criou as classes. Vamos entender os métodos da classe BinaryTree.

Método isEmpty():

Esse método é o mais simples de todos. Para saber se a árvore está vazia ou não, precisamos somente saber se seu root é nulo. Caso ele seja, a árvore estará vazia pois, no root é onde começam as conexões com outros nós.

Método getAltura() e getAltura(Node root):

Esses métodos são sobrecarregados pois, o segundo é recursivo. A recursividade do segundo método se dá pelo fato de que, quando estamos trabalhando com árvore e precisamos percorrê-las, temos que chegar até sua folha da esquerda, depois chegar até sua folha da direita e por último analisar a raiz. Sem recursividade isso não seria possível. Para descobrir a altura, precisamos primeiro descobrir a altura do nó da esquerda, depois do nó da direita e somar 1. É necessário somar 1 pois a altura dos nós folha é 0. 

Precisamos comparar se a altura da esquerdá é maior do que a da direita porque, a altura de uma árvore é o maior caminho da raiz até a folha mais longe. Logo, quanto maior a altura do nó mais longe ele está da raiz. Caso você ainda tenha dúvidas para entender essa função, recomendo que você assita esse vídeo: https://www.youtube.com/watch?v=qVnNdmx4fOA

Método getQtdNode() e getQtdNode(Node root):

Esses métodos são sobrecarregados pelo mesmo motivo que o método getAltura() é sobrecarregado também. Para descobrir a quantidade de nós da árvore, precisamos descobrir a quantidade de nós a esquerda e à direita e somar 1. Somar 1 significa que estamos levando em conta o nó raiz.

Método imprimirArvore() e imprimirArvore(Node node):

Imprime a árvore de forma pós-ordem, ou seja, acessa primeiro nó esquerdo, depois nó direito e por último a raiz. Para cada nó, seu valor é impresso no console.

Tcharammmmmmmm !!! 

Já entendemos quatro métodos da nossa API de árvore binária. Faltam os métodos para inserir e remover. Para realizarmos isso precisamos entender um novo conceito: árvore binária de busca. A árvore binária de busca é um tipo de árvore binária que estabelece que todos os valores à esquerda do nó pai devem ser menores que o mesmo e todos os valores à direita devem ser maiores que o nó pai. Entendeu agora porque eu não quis entrar em detalhes na figura 2 ?

As inserções e remoções devem respeitar essa regra. Caso contrário, a árvore não será mais uma árvore binária de busca.

Falarei de inserção e remoção de valores em árvores binária de busca porque, é o que é mais feito pelos autores em livros. Se quiséssemos estudar a inserção e remoção em árvore binárias comuns, precisaríamos somente saber os conceitos básicos dessa árvore. Dessa forma, você em 1 post aprende dois tipos de árvores.

Método inserir(int valor) e inserir(Node node, int valor):

1. Começo a percorrer a árvore pela raiz
2. Avalio se o valor que está sendo inserido é maior ou menor (não pode ser igual) do que o nó que estou avaliando.
3. Caso seja menor, avalio se já existe um nó na esquerda e repito o passo 2.
4. Caso não haja um nó esquerdo, crio um e gravo o novo valor ali.
5. Caso o valor seja maior do que o nó que estou avaliando, avalio se já existe um nó na direita e repito o passo 2.
6. Caso não haja um nó direito, crio um e gravo o novo valor ali.

Método remover(int valor) e remover(Node node, int valor):

1. Avalio se a raíz é null. Caso seja informo que a árvore está vazia.
2. Caso a raíz não seja null. Avalio se o valor que quero remover é maior ou menor que o nó que estou avaliando (o primeiro nó é a raíz, obviamente).
3. Caso seja menor, acesso o nó esquerdo e faço isso até encontrá-lo.
4. Quando encontro ele, avalio se ele tem filhos à esquerda e à direita.
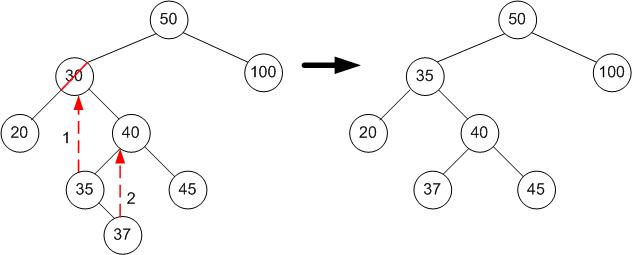
5. Caso tenha, vou para a sub-árvore da direita e procuro o nó de menor valor à esquerda. Depois de encontrá-lo, atribuo o valor desse menor nó ao nó que está sendo excluído (ver imagem 5).
6. Depois da atribuição do passo 5 ter sido feita, eu preciso refazer a ligação que o pai do menor nó à esquerda tinha pois, agora o pai dele vai apontar para null.
7. O valor passado como parâmetro foi excluído.
8. Ao contrário do passo 3, ou seja, o valor é maior, acesso o nó direito e faço isso até encontrá-lo.
9. Repito os passos 4 à 7.
10. Caso um nó seja folha ou só tenha 1 filho, removo seu valor e atualizo seu pai.

Para ficar mais fácil, olhe as imagens 3, 4 e 5.

Figura 3 - Excluindo nó folha - http://upload.wikimedia.org/wikipedia/commons/6/6c/Bstreedeleteleafexample.jpg

Figura 4 - Excluindo nó com 1 filho - http://upload.wikimedia.org/wikipedia/commons/6/6a/Bstreedeleteonechildexample.jpg

Figura 5 - Excluindo um nó com dois filhos - http://upload.wikimedia.org/wikipedia/commons/1/15/Bstreedeletenotrightchildexample.jpg

Bem amigos, esse post ficou grande mas, espero que esteja tudo bem explicado.

Terminamos !! Ufa !! 

Sugestões ?! Críticas ?! Elogios ?! 

Deixe aí nos comentários ou na nossa página do facebook.

Facebook: https://www.facebook.com/precisoestudarsempre/

Referências:

[ED] Aula 67 - Árvores - https://www.youtube.com/watch?v=iLvpaqAoVD8

[ED] Aula 69 - Árvore Binária: Definição - https://www.youtube.com/watch?v=9WxCeWX9qDs

[ED] Aula 70 - Árvore Binária: Implementação - https://www.youtube.com/watch?v=TR8ZLUKmcPc

[ED] Aula 72 - Árvore Binária: informações básicas - https://www.youtube.com/watch?v=qVnNdmx4fOA

[ED] Aula 73 - Percorrendo uma Árvore Binária - https://www.youtube.com/watch?v=z7XwVVYQRAA

[ED] Aula 74 - Árvore Binária de Busca - https://www.youtube.com/watch?v=M7cb4HjePJk

[ED] Aula 75 - Inserção em Árvore Binária de Busca - https://www.youtube.com/watch?v=8cdbmsPaR-k

[ED] Aula 76 - Remoção em Árvore Binária de Busca - https://www.youtube.com/watch?v=_0Yu9BSYXGY

https://www.cs.usfca.edu/~galles/visualization/BST.html

http://manfred.com.br/index.php/bsi/estrutura-de-dados-i/144-aula-12-exclusao-de-um-no-em-arvore-binaria-e-arvore-avl-em-java

http://pt.wikipedia.org/wiki/%C3%81rvore_bin%C3%A1ria_de_busca

http://javafree.uol.com.br/topic-882029-Arvore-binaria.html