Árvores geradoras mínimas - Grafos

Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.

Esta é a quarta publicação da série Grafos, onde abordaremos mais um assunto desta incrível teoria. Caso você seja novo por aqui e não leu nenhuma postagem ainda, recomendo que você clique aqui e comece pela primeira publicação desta série, onde entendemos o que é um grafo e do que ele é composto. Mas, se você já é um leitor assíduo do blog e leu a penúltima postagem, se delicie agora com mais um conteúdo voltado para você, amante do estudo.

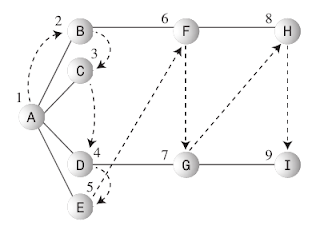
Na teoria dos grafos, as árvores geradoras mínimas servem para gerar representações onde, o foco é eliminar o excesso de arestas. Entenda por excesso o fato de existirem mais arestas que o necessário para conectar o grafo inteiramente. A Figura 1 mostra um grafo com oito vértices e um número excessivo de arestas, ao passo que a Figura 2 mostra um grafo com os mesmos oito vértices, mas com um número mínimo de arestas necessárias para conectá-lo de forma completa.

Figura 1 - Grafo com arestas em demasiado

Figura 2 - Árvore geradora mínima do grafo acima

Diferentes árvores podem ser geradas a partir do momento que escolhemos pontos de partidas diferentes. No nosso caso, o ponto de partida escolhido foi o nó A, logo o resultado só pode ser este, mas caso escolhêssemos o nó B, o resultado seria outro completamente diferente.

Lembre-se que nossa preocupação aqui não é o comprimento das arestas, não estamos tentando encontrar o menor caminho, e sim reduzir a quantidade de arestas (LAFORE, ROBERT).

Outro ponto a ser notado é a possibilidade de se calcular o número de arestas de uma árvore geradora mínima através da expressão abaixo, onde E é a quantidade de arestas e V é a quantidade de vértices.

E = V - 1

Quais seriam as aplicações possíveis para uma árvore mínima geradora ? Muitas, basta somente um pouco de reflexão sobre os problemas do cotidiano. Imagine uma imensa rede de transmissões de linhas telefônicas que conecte todas as cidades de um país. Uma cidade pode se conectar diretamente ou indiretamente a outra cidade, por exemplo Rio de Janeiro - Belo Horizonte ou Rio de Janeiro - São Paulo - Belo Horizonte. Em um determinado momento é decretada uma ordem de redução de custos de cabeamento pelo presidente da empresa, e todas as conexões redundantes precisam ser eliminadas, logo a conexão direta Rio de Janeiro - Belo Horizonte teria seu fim decretado, visto que a conexão alternativa (RJ - SP - BH) atinge o mesmo propósito e ainda traz outra cidade para o novo grafo de conexões.

Este exemplo pode parecer um pouco incomum visto que este presidente estaria jogando o dinheiro da companhia fora quando manda remover os cabos e que talvez as distâncias entre as cidades não compensariam tal trabalho. Porém, isto é somente um exemplo imaginário de um problema real.

O algoritmo usado para criar a árvore geradora mínima é quase idêntico ao usado para buscar. Ele pode ser tanto baseado na busca em profundidade quanto na busca em largura. Neste post, abordaremos uma implementação baseada na busca em profundidade (LAFORE, ROBERT), pois o caminho armazenado na pilha desse tipo de busca é automaticamente a árvore geradora mínima. A única diferença entre a busca e o algoritmo da árvore geradora mínima é que o segundo deve registrar de alguma forma as arestas pelas quais passa.

Um outro motivo da árvore geradora mínima ser facilmente derivada da busca em profundidade é porque essa busca visita todos os nós, mas apenas uma vez. Ele nunca vai para um nó que já tenha sido visitado. Quando ele ver uma aresta que tenha um nó visitado no final, não irá segui-la. Ele nunca viaja por uma aresta que não seja necessária. Assim, o caminho percorrido pela busca tem que ser uma árvore geradora mínima (LAFORE, ROBERT).

Escolhi Java como a linguagem de programação para estes algoritmos por uma questão de afinidade, mas nada impede que você utilize uma versão do Java diferente da minha ou até outra linguagem.

Este é o método responsável pela geração da árvore geradora mínima. Como dito antes, este algoritmo se assemelha muito com o algoritmo de busca em profundidade, e isto é visível no trecho de código acima. A única diferença que deve ser ressaltada é a exibição dos nó atual e o adjacente à ele juntamente com o espaço em branco, o qual facilita a visualização do resultado final.

Caso você não tenha conhecimento sobre as buscas em profundidade, já abordamos esse assunto aqui no blog. Clique aqui e tire suas dúvidas. Recomendo a leitura.
A classe acima tem como propósito final criar e montar um grafo para depois executar a geração da árvore mínima geradora nele. O resultado esperado, como já visto na Figura 2, é um grafo com o mínimo de arestas possíveis que conectem todos os seus vértices.

Chegamos ao fim de mais uma postagem da série Grafos. Ainda temos muito conteúdo para discutir e muitas coisas novas para aprender, estamos somente no início de uma longa jornada. Então se prepare para as novidades que vem por aí.

Até a próxima minha boa gente ! 😘

Leia nossa postagem anterior: Busca em largura - Grafos

Download do código-fonte
Link do repositório GitHub: https://github.com/PrecisoEstudarSempre/Graphs.git

Dúvidas !? Sugestões ?! Críticas ou elogios ?!

Deixe aí nos comentários, envie um e-mail ou uma mensagem na nossa página do Facebook.

E-mail: precisoestudarsempre@gmail.com
Facebook: https://www.facebook.com/precisoestudarsempre/
Canal Preciso Estudar Sempre: https://www.youtube.com/channel/UCUoW8dS38rXr0a5jWU57etA

Referências

LAFORE, ROBERT; Estruturas de Dados e Algoritmos em Java; 2004

Leia Mais ››

Busca em largura - Grafos

Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.

Na nossa última postagem abordamos uma das formas de se realizar uma busca em um grafo, a busca em profundidade. Caso você não tenha lido, clique aqui. Mas, se você for um total iniciante no assunto, recomendo que você comece lendo a primeira postagem dessa nova série, clicando aqui.

Já informo de antemão que utilizarei a linguagem de programação Java para a construção das implementações dos algoritmos e que nada impede que você utilize uma outra versão do Java diferente da minha ou, até uma outra linguagem. Agora, sem mais delongas, vamos ao assunto.

A necessidade e as restrições que envolvem este assunto são as mesmas que envolviam o assunto da postagem anterior. Dado um grafo G desconhecido, quais nós são possíveis de atingir a partir de um determinado nó N ? Esta pergunta, obviamente, já foi respondida, mas aqui veremos uma outra forma de respondê-la.

Analisemos o grafo mostrado na Figura 1.

Figura 1 - Grafo de exemplo

Assim como já foi discutido previamente, é necessário que um ponto de partida seja escolhido, pois o grafo analisado é desconhecido de primeira mão, estamos às cegas. Só teremos o conhecimento de um ponto inicial, o nó A no nosso caso. Tal condição não somente viabiliza a pergunta feita acima, mas como nos deixa à frente de grandes problemas, como: O que fazer ? Qual nó adjacente visitar primeiro ?

Ao contrário de sua irmã, a busca em largura não visita a fundo todo um caminho de arestas até chegar em um ponto que não consiga ir mais adiante, ela se comporta de uma forma completamente diferente. Ela visita todos os nós adjacentes ao nó inicial e apenas então vai mais adiante. A estrutura que serve como alicerce para tudo isso é uma fila do tipo FIFO, pois é ela que vai registrar qual é o caminho atual percorrido. Caso você não seja conhecedor de tal estrutura, recomendo fortemente o estudo dela antes de continuar a leitura deste post e peço desculpas por não deixar uma referência de post do próprio blog sobre o assunto. Não faço isso, pois ainda não abordei esse tema.😞

Imagine o seguinte: uma pedra cai na água de uma calma lagoa (LAFORE, ROBERT). Quando a pedra entra em contato com a água, ela cria ondas que se espalham de forma igual por toda a superfície criando assim um fenômeno homogêneo. Tal característica se repete nas buscas em largura, ou seja, os nós são percorridos de uma forma igual em relação às suas adjacências. Isto significa que todos os nós que estão a uma aresta de distância do ponto inicial são encontrados primeiro, então todos os nós que estão a duas arestas de distância são encontrados em seguida, e etc. Tal característica será útil se você estiver tentando encontrar o caminho mais curto do nó inicial até um determinado nó (LAFORE, ROBERT).

Para uma execução organizada e procedural, três regras foram criadas. São elas:

Regra 1
Visite o próximo nó não visitado, se existir, que seja adjacente ao nó atual, marque-o e insira-o na fila (LAFORE, ROBERT).

Lembre que nosso ponto de partida é o nó A, já temos conhecimento sobre ele, logo nenhum processamento a mais é necessário. Tal fato nos permite a executar a regra 1, o que nos leva ao nó B. Após isso, devemos verificar se A não possui nenhum outro nó adjacente não visitado ainda, e então descobrimos C, D e E. Para estes três últimos nós, a regra 1 deve ser aplicada. Agora na fila temos: B C D E.

Após executar a regra 1 para todos os nós adjacentes à A, não teremos mais nós adjacentes não visitados. Então, o que fazer ? Para esta necessidade surge a regra 2.

Regra 2
Se você não puder executar a Regra 1 porque não há mais nó não visitado, remova um nó da fila e torne-o o nó atual (LAFORE, ROBERT).

Removendo um nó da fila teremos B, mas porque não E ? Isto acontece devido ao tipo de fila que estamos utilizando. A sigla FIFO significa first-in-first-out, ou seja, o primeiro que entra é o primeiro que sai, assim como na fila de um banco. Logo, filas que usem esse tipo de esquema de organização de itens terão este comportamento, e este é o nosso caso.

Voltando à nossa linha de raciocínio, remover um nó da fila resultará no nó B, e este é o nosso nó atual. Uma nova execução da regra 2 se faz necessária, mas agora é possível executar a regra 1 pois o nó atual possui nós adjacentes não visitados. Isto fará com que F entre na fila.

C sai da fila, não possui adjacências. Devemos remover o próximo pois a regra 1 não consegue ser satisfeita, logo removemos D da fila. A partir deste, enfileiramos G e concluímos que assim como C, o nó E sai da fila e não possui adjacências.

A interação entre a regra 1 e a regra 2 recria o fenômeno de onda citado anteriormente, pois as adjacências de F e G só serão exploradas totalmente quando todos os nós que estão no mesmo “nível” de seus pais forem exploradas primeiro.

A regra 2 é executada em F, menos um na fila e em seguida H é enfileirado pela regra 1. O mesmo acontece para I quando G é desenfileirado. Execuções contínuas da regra 2 em conjunto da 1 resultarão em uma fila vazia, o que nos leva à regra 3.

Regra 3
Se não puder executar a Regra 2 é porque a fila está vazia, terminou (LAFORE, ROBERT).

Visto que houveram muitas movimentações na fila durante a execução das regras, a Tabela 1 mostra de forma detalhada o passo a passo de todas as operações realizadas.

Evento	Fila
Vá para A
Vá para B	B
Vá para C	BC
Vá para D	BCD
Vá para E	BCDE
Remova B	CDE
Vá para F	CDEF
Remova C	DEF
Remova D	EF
Vá para G	EFG
Remova E	FG
Remova F	G
Vá para H	GH
Remova G	H
Vá para I	HI
Remova H	I
Remova I
Terminado

Se você leu o post anterior sobre busca em profundidade notará que as diferenças são grandes. Compare como as duas abordagens funcionam e deixe sua opinião nos comentários.👍

Visto que já conhecemos toda a teoria necessária para entender e executar uma busca em largura, podemos a partir daí transcrever este algoritmo para um programa Java.

Este método executa as três regras descritas acima de uma forma bem simples. Ele inicia adicionando o primeiro nó do grafo, o ponto de partida, na fila, e partir daí verifica repetidamente se a fila não está vazia. Caso negativo a busca chegou ao fim pois não existem mais nós para analisar, mas caso contrário, ainda existem nós não explorados e os processos descritos nas regra 1 e 2 são executados.

É possível notar que um método auxiliar é utilizado para verificar as adjacências de um determinado nó. Por tal motivo, o segundo laço de repetição se faz necessário pois um nó pode ter N adjacências.

O último laço de repetição utilizado tem a finalidade de somente resetar a flag de visitação dos nós para que buscas futuras possam ser executadas sem problemas.

O método getAdjUnvisitedVertex(vertexIndex) é responsável para um determinado nó obter seus nós adjacentes não visitados, conforme citado acima. Sua implementação é simples e tem apoio da matriz de adjacência e da flag de visitação para a recuperação da informação desejada. Caso encontre, retorna a posição deste nó no array de nós, caso contrário, retorna -1 simbolizando que não encontrou nada.

Ambos os métodos fazem parte de uma classe que foi criada em postagens passadas. Logo, os detalhes que já foram incorporados não serão abordados aqui. Para que você tenha uma visão geral de tudo feito até agora, faça o download do projeto usando o link do repositório no fim do post.

A classe acima é somente utilitária. Sua única responsabilidade é criar e montar um grafo para depois executar a busca em largura nele. O resultado esperado de sua execução é o caminho percorrido pelo algoritmo de busca.

Esta postagem é somente mais uma que compõe a grande série de assuntos envolvendo a teoria dos grafos. Em publicações futuras veremos árvores geradoras mínimas, o algoritmo de Warshall e etc.

Até a próxima minha boa gente ! 😘

Leia nossa última postagem sobre grafos: Busca em profundidade - Grafos

Download do código-fonte
Link do repositório GitHub: https://github.com/PrecisoEstudarSempre/Graphs.git

Dúvidas !? Sugestões ?! Críticas ou elogios ?!

Deixe aí nos comentários, envie um e-mail ou uma mensagem na nossa página do Facebook.

E-mail: precisoestudarsempre@gmail.com
Facebook: https://www.facebook.com/precisoestudarsempre/
Canal Preciso Estudar Sempre: https://www.youtube.com/channel/UCUoW8dS38rXr0a5jWU57etA

Referências

LAFORE, ROBERT; Estruturas de Dados e Algoritmos em Java; 2004

Leia Mais ››

Busca em profundidade - Grafos

Bem-vindos ao blog Preciso Estudar Sempre. Meu nome é João Paulo Maida e minha paixão é estudar.

Comecemos esta postagem com a seguinte pergunta: Em um grafo desconhecido, quais nós são possíveis de atingir a partir de um determinado nó ?

A resposta é simples. A partir de um nó inicial é possível atingir qualquer nó que esteja conectado à ele diretamente ou às suas adjacências por arestas. Esta regra é válida para qualquer nó. Contudo, o processo para chegar a essa conclusão não é tão trivial assim, pois os casos em que isto precisa ser determinado são aqueles que o único conhecimento disponível é sobre um nó inicial, ou seja, um ponto de partida.

Caso você tenha chegado a este ponto do texto não entendendo muito do que já foi explicado, recomendo fortemente que você leia nossa primeira postagem sobre a teoria dos grafos. Clique aqui para dar uma conferida.

A construção desse processo consiste em passos sistemáticos que possibilitam a movimentação de um vértice para outro, e assim de pouco em pouco espera se obter o conhecimento completo do grafo. Existem atualmente duas abordagens conhecidas para este tipo de processo: busca em profundidade (DFS - Depth First Search) e busca em largura (BFS - Breadth First Search). Ambas finalmente alcançarão todos os nós conectados. A primeira busca, alvo do nosso estudo, é implementada com uma pilha, ao passo que a segunda é implementada com uma fila. Esses mecanismos resultarão no grafo sendo percorrido de maneiras diferentes (LAFORE, ROBERT).

A pilha citada no parágrafo acima é uma estrutura que já foi abordada aqui no blog. Caso você a conheça pule este parágrafo, mas caso contrário, clique aqui e dê uma lida antes de continuar nesta postagem.

Descobrir a solução para a pergunta acima assombrou por muito tempo os estudiosos da teoria dos grafos, mas o matemático francês Charles Pierre Trémaux, no século XIX, propôs uma versão da busca em profundidade como estratégia para resolver labirintos.

Figura 1 - O labirinto

Pode parecer complicado comparar labirintos com grafos, mas com um pouco de abstração é possível notar que um pode ser sim representado no outro. Para a entrada do labirinto temos o nó inicial de um grafo, para o término de um caminho ou ramificação temos mais nós, e para os caminhos que interligam todos esses três elementos temos as arestas. Um dos segredos para sair de um labirinto é lembrar o caminho feito e geralmente isso é feito usando um barbante. O herói grego Teseu utilizou desta mesma técnica quando enfrentou o terrível Minotauro em seu imenso labirinto. A busca em profundidade utiliza a mesma idéia, mas ao invés do barbante utilizaremos a pilha, já citada anteriormente.

Figura 2 - O labirinto do Minotauro

O algoritmo que procuramos nos dará certeza que o grafo será complemente escaneado sem que percamos tempo com escolhas erradas, e que após todo o procedimento ter sido feito ele terminará sua execução. Contudo, para realizar tal façanha nenhum pré-planejamento pode ser feito, visto que não temos conhecimento sobre sua estrutura. Então, decisões de direção devem ser tomadas uma após a outra ao longo do trajeto feito (EVEN, SHIMON). Por tais motivos a dúvida apresentada no início da postagem é justificada.

Analisemos a Figura 3 para que possamos tomar conhecimento de como a busca em profundidade funciona.

Figura 3 - Grafo de exemplo

A determinação de um ponto de partida é necessária e já foi citado acima, logo para o grafo da Figura 3 temos o nó A representando esse papel. Neste momento a única informação que temos é que apenas este nó compõe o grafo. Então, precisamos executar três passos essenciais: visitar o nó, colocá-lo na pilha para que possamos lembrar no futuro que já passamos por ali, e marcá-lo como visitado. Tudo isto dá vida à Regra 1.

Regra 1
Se possível, visite um nó adjacente não visitado, marque-o e coloque-o na pilha.

Executando esta regra, partimos de A em direção ao nó B. Em B executamos a regra 1 novamente e partimos em direção à F. O processo novamente se repete e vamos de F para H. O nó H não possui adjacências, e logo estamos parados. Então, o que fazer agora? Neste momento surge a regra 2.

Antes de abordarmos a regra 2 note que a denominação “profundidade” vem do efeito que a regra 1 causa no ato da movimentação do grafo. Note que exploramos toda uma ramificação de nós e arestas para assim depois decidir o que fazer. Essa característica será drasticamente modificada quando abordarmos as buscas por larguras.

OBSERVAÇÃO: O nó inicial também entra nesta regra mesmo não sendo adjacente.

Regra 2
Se você não puder seguir a Regra 1, então se possível, retire um nó da pilha.

Seguindo esta regra, desempilhamos H e voltamos para F, logo em seguida para B e finalmente para A. Executamos todo esse caminho de volta porque não foi possível executar a Regra 1, visto que todo este caminho já tinha sido explorado. Note que o uso da pilha tem imensa importância, pois ele age como se fosse o barbante de Teseu, ele mostra o caminho de volta. Quando chegamos em A, a Regra 1 se torna disponível mais uma vez pois este possui vários filhos. Então de A vamos para C e de C voltamos para A. A partir deste, o próximo destino é D.

O nó D por sua vez possui adjacências e a partir dele vamos para G e depois para I. Após chegar neste ponto, voltamos novamente para A, para finalmente ir para E e finalizar em A pela última vez.

Agora não temos mais o que fazer, já percorremos o grafo inteiro saindo de um ponto inicial e terminando o trajeto nele. Eis que surge a Regra 3.

Regra 3
Se você não puder seguir a Regra 1 ou a 2, então terminou.

A tabela abaixo mostra todas as operações realizadas na pilha enquanto o passo-a-passo, descrito acima, foi sendo feito.

Evento	Pilha
Vá para A	A
Vá para B	AB
Vá para F	ABF
Vá para H	ABFH
Volte para F	ABF
Volte para B	AB
Volte para A	A
Vá para C	AC
Volta para A	A
Vá para D	AD
Vá para G	ADG
Vá para I	ADGI
Volte para G	ADG
Volte para D	AD
Volte para A	A
Vá para E	AE
Volte para A	A
Desempilhe A
Terminado

Visto que já conhecemos todos os passos necessários para executar a busca em profundidade, podemos agora ver sua implementação em Java. Repito novamente, que utilizo esta linguagem de programação por uma questão de afinidade, e nada impede que você implemente este mesmo algoritmo em uma outra linguagem de seu gosto.

A implementação se torna bem simples quando temos as regras em mente. O primeiro bloco, linhas 2 à 4, executam a regra 1 para o nó ponto de partida. Não necessariamente o seu nó de partida deve ser o primeiro item do array. Isto foi feito com a finalidade de facilitar a implementação do algoritmo.

O loop que segue da linha 7 até 16 perpetua a regra 1 e insere a regra 2 no programa. O próximo nó adjacente não visitado é obtido através de uma função específica que retorna a posição deste no array de nós. Caso o nó não exista, a regra 2 entra em ação. Caso contrário, o processo continua conforme descrito na regra 1. A implementação desta função não foi incorporada na função de busca porque havia o receio do código ficar muito extenso e isso atrapalhar a análise do algoritmo.

O último laço reseta a flag de visitação de todos os nós para que a busca possa ser executada posteriormente.

O método getAdjUnvisitedVertex(vertexIndex) é responsável para um determinado nó obter seus nós adjacentes não visitados, conforme citado acima. Sua implementação é simples e tem apoio da matriz de adjacência e da flag de visitação para a recuperação da informação desejada. Caso encontre, retorna a posição deste nó no array de nós.

Ambos os métodos fazem parte de uma classe que foi criada em postagens passadas. Logo, os detalhes que já foram incorporados não serão abordados aqui. Para que você tenha uma visão geral de tudo feito até agora, faça o download do projeto usando o link no fim do post.


A classe acima é somente utilitária. Sua única responsabilidade é criar e montar um grafo para depois executar a busca em profundidade nele. O resultado esperado de sua execução é o caminho percorrido pelo algoritmo de busca.

Nas referências é possível encontrar um excelente trabalho feito pela Universidade Federal da Paraíba, onde é proposto a criação de um labirinto aleatório através da aplicação de um algoritmo de busca em profundidade. Para fornecer as outras respostas do labirinto, como a saída e o menor caminho, outros algoritmos são utilizados. Vale a pena a leitura.

Até a próxima minha boa gente ! 😘

Leia nossa última postagem sobre grafos: Matrizes de adjacência e grafos

Download do trabalho da UFPB: https://drive.google.com/file/d/0BzDmhBY6luU6dktwUXhydTIxcms/view?usp=sharing

Download do código-fonte
Link do repositório GitHub: https://github.com/PrecisoEstudarSempre/Graphs.git

Dúvidas !? Sugestões ?! Críticas ou elogios ?!

Deixe aí nos comentários, envie um e-mail ou uma mensagem na nossa página do Facebook.

E-mail: precisoestudarsempre@gmail.com
Facebook: https://www.facebook.com/precisoestudarsempre/
Canal Preciso Estudar Sempre: https://www.youtube.com/channel/UCUoW8dS38rXr0a5jWU57etA

Referências

LAFORE, ROBERT; Estruturas de Dados e Algoritmos em Java; 2004

EVEN, SHIMON; Graph Algorithms; 2012

MENEZES, RÔMULO; MACHADO, LILIANE; MEDEIROS, ÁLVARO; Aplicação de Algoritmos de Grafos para Gerar e Percorrer Jogos de Labirintos Aleatórios; Universidade Federal da Paraíba

Leia Mais ››